Взвешенное скользящее среднее

Взвешенное скользящее среднее (англ. Weighted Moving Average, сокр. WMA) – это один из вариантов простого скользящего среднего, где учитываются не только значения цен, но и их значимость (вес).

Рассчитывается по формуле:

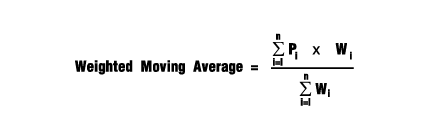
где: Pi – значения цены за количество i-периодов, (i сегодня =1),
Wi – значения весов для цены за количество i-периодов.

Проще говоря, элементы с учетом их значимости суммируются между собой и делятся на сумму весов этих элементов, то есть в самом общем виде рассчитывается средняя арифметическая этих элементов.

По умолчанию принято считать, что вес изменяется по линейной функции, где W1 присваивается наибольший вес и далее расчет ведется с использованием простой арифметической прогрессии, например: 1, 2, 3, 4, 5, 6…; (или любая другая: 0,5, 0,75, 1, 1,25). Такой вид именуется линейно-взвешенная скользящая средняя (англ. Linear Weighted Moving Average, сокр. LWMA). Для примера, возьмем период, равный пяти:

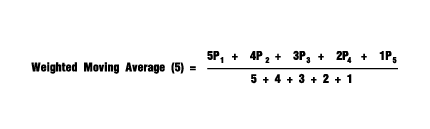
где: P1 и P2 – это цены сегодня и вчера соответственно.

В некоторых модификациях могут быть использованы и более сложные формулы, где распределение ведется нелинейным образом, а с использованием логарифмических, параболических и других функций, например если в расчет берутся:
– количество тиков в баре;
– размер пройденного расстояния в свече (High – Low)
– среднее взвешенное по расстоянию; – размер тела свечи (|Close – Open|).

Цены также могут быть различными: Close, Open, High, Low, Median Price, Typical Price.

Применение WMA

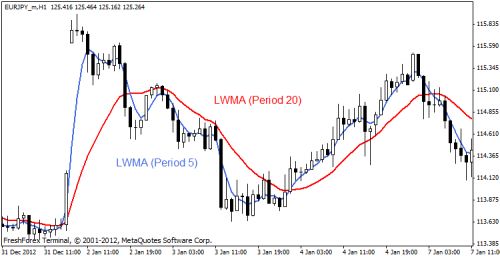
Взвешенное скользящее среднее на примере

Взвешенное скользящее среднее обычно применяют в тех же случаях, что и простое скользящее среднее в техническом анализе рынка. Однако при схожих сигналах на вход и выход из рынка LWMA быстрее реагирует на изменение цен, поскольку значимость (вес) придается последним периодам. Это позволяет не упускать удачные моменты входа во время выхода важных экономических новостей, интервенций и других крупных движений.

Для фондового рынка рекомендуется использовать параметры, равное 7 и 14. Для валютного – 5 и 20. Как видно на рисунке, чем больше период, тем более плавное среднее скользящее и тем меньший диапазон колебаний оно имеет.

Синус-взвешенное скользящее среднее (англ. Sine-Weighted Moving Average, сокр. SWMA) при его расчете в качестве W (веса) используется синусная функция. С помощью SWMA можно фильтровать шумы, более точно определять дно и вершины.

Преимущества и недостатки WMA

Благодаря учету значимости (веса) элементов, WMA более чутко реагирует на изменение цен, чем простое скользящее среднее, что позволяет быстрее получать сигналы на вход и выход из тренда. Однако, как и любое другое MA, взвешенное также имеет некое запаздывание.

Лучше всего применять в краткосрочных и среднесрочных стратегиях, поскольку наибольший вес имеют последние значения цены. Проще говоря, на высоких таймфреймах WMA выглядит более сглаженной из-за низкого шума рынка, и оно не дает столь четких сигналов.

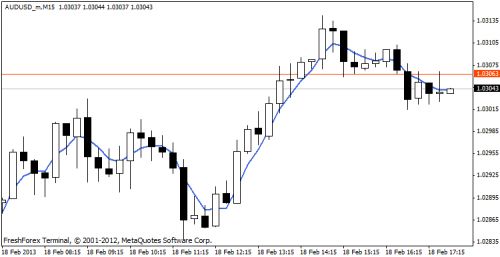
WMA более чутко реагирует на изменение цен

WMA лучше всего применять в краткосрочных и среднесрочных стратегиях